En esta serie de artículos, analizaremos uno de los papers más influyentes de la criptografía moderna: "A Decade of Lattice Cryptography" (Una Década de Criptografía de Retículos) de Chris Peikert. Este documento es fundamental porque describe la base matemática de la mayoría de los sistemas criptográficos diseñados para resistir ataques de computadoras cuánticas.
La criptografía que usamos hoy (como RSA) se romperá con las computadoras cuánticas. Los retículos son la principal alternativa, ya que no se conocen algoritmos cuánticos eficientes para romperlos.
Pero, ¿qué es un retículo? Antes de entrar en las matemáticas complejas, comencemos con una intuición visual.
¿Qué es un Retículo?
En su forma más simple, un retículo (o lattice) es una cuadrícula infinita de puntos, dispuesta de forma perfectamente regular en el espacio. Piensa en una hoja de papel cuadriculado infinita; las esquinas de los cuadrados forman un retículo de 2 dimensiones.

Subtítulo: Visualización de un retículo: una cuadrícula infinita de puntos equidistantes en el espacio.
El paper nos da una definición más formal en la Sección 2.2.1: un retículo L es un subconjunto de puntos en un espacio Rn que cumple dos propiedades:
Es un subgrupo aditivo: Si tomas dos puntos cualesquiera del retículo y los sumas, el resultado es otro punto dentro del mismo retículo.
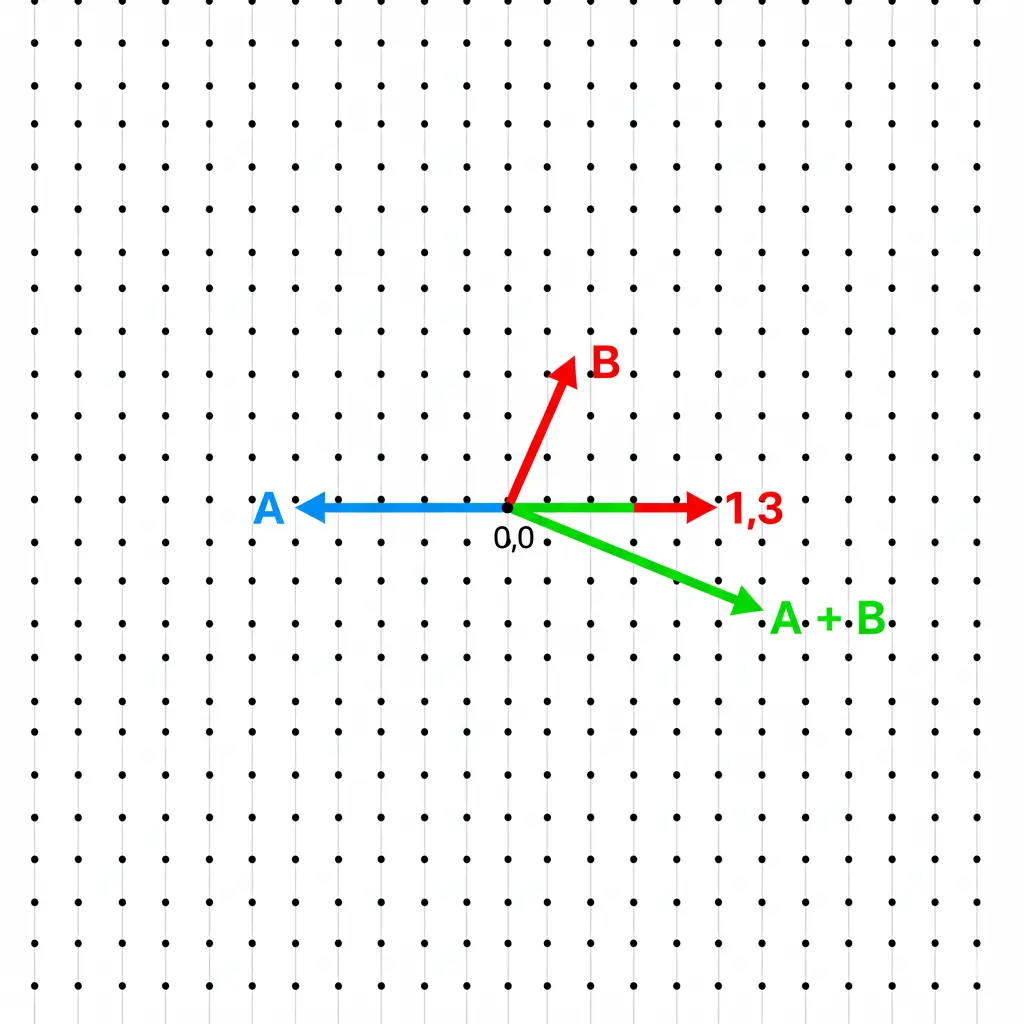
Subtítulo: Propiedad de subgrupo aditivo: La suma de dos puntos (vectores) del retículo, A + B, resulta en otro punto que también pertenece al retículo.
Es discreto: Cada punto está "aislado", con un espacio vacío a su alrededor que no contiene ningún otro punto del retículo.
El ejemplo más básico es Zn, que es simplemente la cuadrícula de todos los puntos con coordenadas enteras.
La Clave Secreta: Bases "Buenas" vs. "Malas"
Todo retículo es generado por un conjunto de "vectores base" B. Piensa en ellos como las instrucciones para construir la cuadrícula: "ve dos pasos al norte, luego un paso al este".
Aquí está el concepto más importante de toda la criptografía de retículos: una base no es única. El mismo retículo exacto puede ser generado por infinitas bases diferentes.
Esto crea una asimetría fundamental que el paper menciona en la Sección 3.3:
Una Base "Buena" (la Clave Secreta): Consiste en vectores cortos y casi perpendiculares entre sí. Es como un simple mapa de cuadrícula. Con esta base, es fácil trabajar y encontrar puntos..
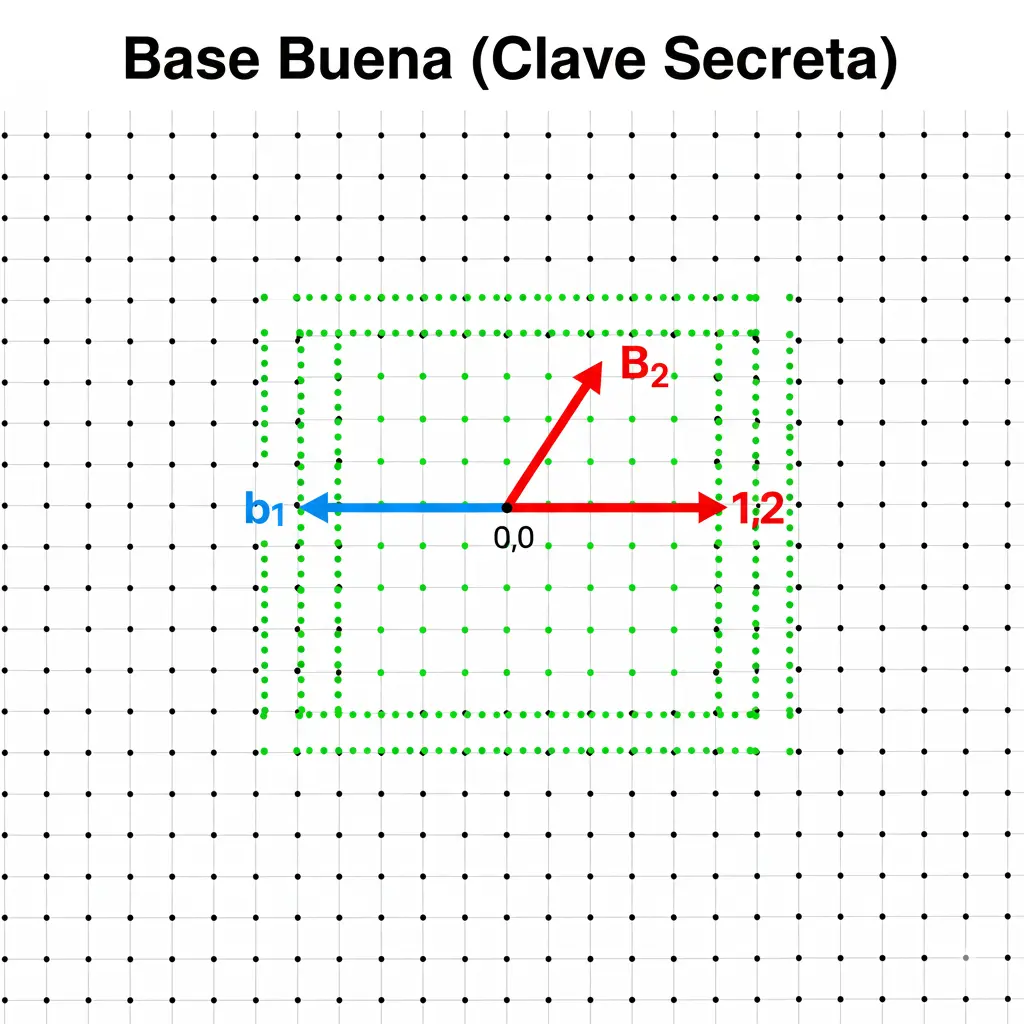
Subtítulo: Una "base buena" (la clave secreta) consiste en vectores cortos y casi perpendiculares (ortogonales), haciendo que la estructura del retículo sea fácil de ver.
Una Base "Mala" (la Clave Pública): Consiste en vectores muy largos y en ángulos extraños. Genera la misma cuadrícula de puntos, pero de una manera caótica y distorsionada.
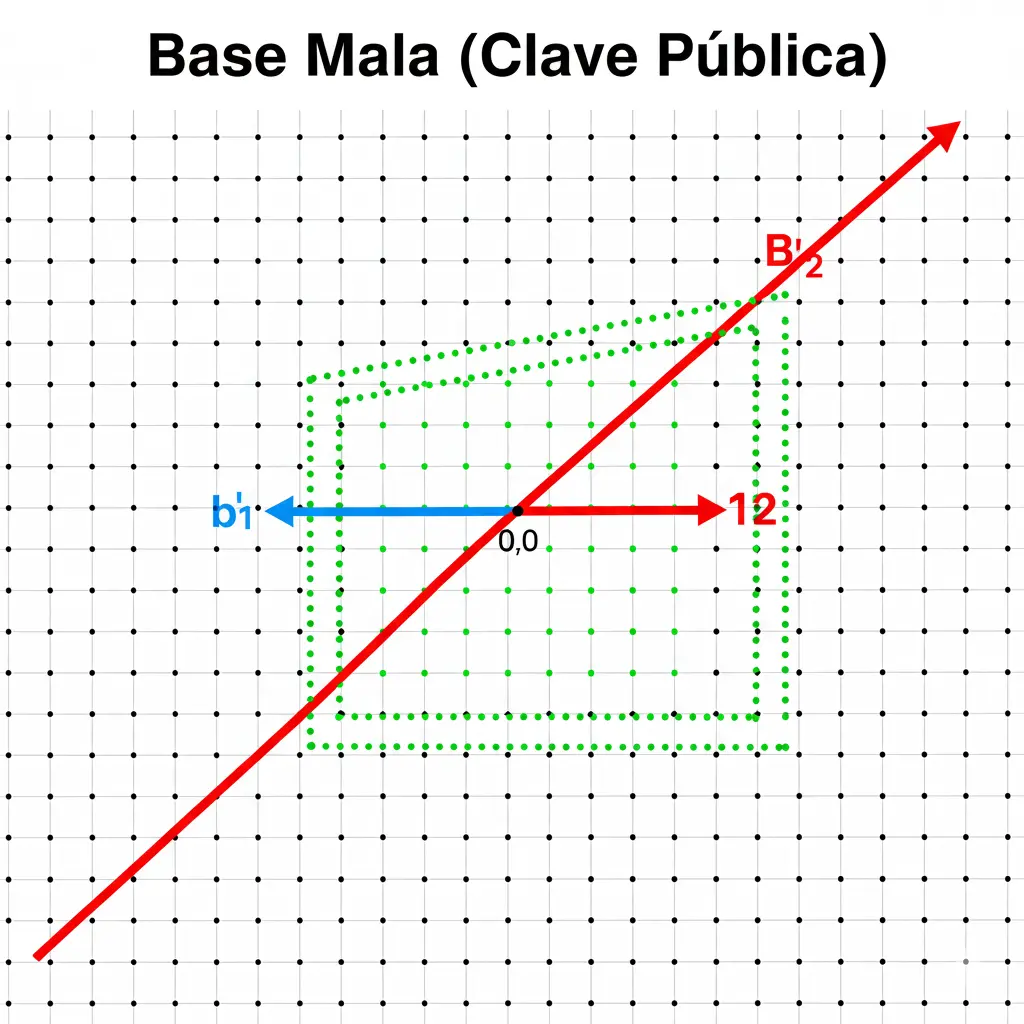
Subtítulo: Una "base mala" (la clave pública) genera el mismo retículo, pero con vectores largos y en ángulos no perpendiculares, ocultando su verdadera estructura.
Imagina que quieres ir a un punto. Con la base "buena", el camino es directo. Con la base "mala", tienes que dar un rodeo increíblemente complicado. La seguridad de los retículos se basa en que, si solo tienes la base "mala" (la clave pública), ciertos problemas son computacionalmente imposibles de resolver.
Los Problemas Difíciles de los Retículos
La dureza de los retículos se basa en problemas que parecen simples de describir pero son increíblemente difíciles de resolver si solo tienes una base "mala". El paper define los más importantes en la Sección 2.2.2:
1. SVP (Shortest Vector Problem - Problema del Vector Más Corto)
La Pregunta: Dado un retículo (a través de una base "mala"), encuentra el punto más cercano al origen (sin contar el propio origen).
La Intuición: Te entrego un mapa caótico (la base "mala") de una ciudad. Te reto a encontrar la casa más cercana al ayuntamiento (el origen). Como el mapa está distorsionado, cualquier camino que intentes seguir parece larguísimo. Encontrar el verdadero atajo más corto λ1(L) es intratable en altas dimensiones.
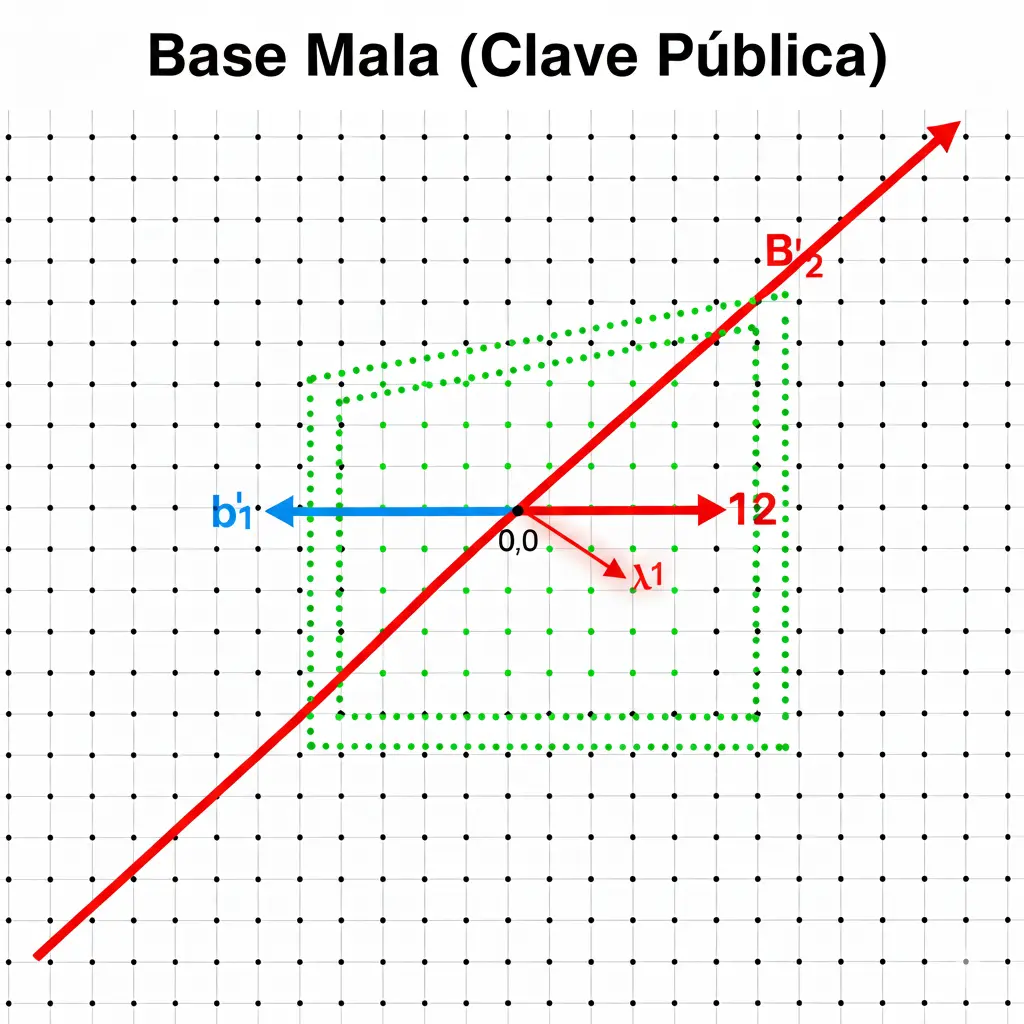
Subtítulo: El Problema del Vector Más Corto (SVP): Dada una "base mala" (pública), es computacionalmente difícil encontrar el vector más corto del retículo, λ₁
2. BDD (Bounded Distance Decoding - Decodificación de Distancia Acotada)
La Pregunta: Te doy un retículo (la base "mala") y un punto t que no está en la cuadrícula. Se te promete que este punto t está muy, muy cerca de un único punto v del retículo. Tu tarea es encontrar v.
La Intuición: Este es el problema de "eliminar el ruido". Piensa que v es una señal digital perfecta, e es un pequeño "ruido" aleatorio, y tú recibes t=v+e. Tu trabajo es recuperar la señal original v. Si solo tienes la base "mala", es casi imposible saber a cuál de los infinitos puntos de la cuadrícula pertenece ese ruido.

Subtítulo: El Problema de Decodificación de Distancia Acotada (BDD): Se recibe un punto t (señal con ruido) y se debe encontrar el punto v (señal original) más cercano en el retículo. La diferencia es el vector de "ruido" e .
Conclusión
La criptografía de retículos se basa en esta poderosa asimetría: es fácil crear un problema (generando una base "buena" y luego "escondiéndola" para crear una "mala"), pero es imposible resolverlo sin conocer la base "buena" original (la clave secreta).
Estos problemas, SVP y BDD, son los cimientos. En el próximo artículo, veremos cómo el Capítulo 4 del paper utiliza estos problemas para construir los dos pilares algorítmicos de la criptografía post-cuántica: SIS y LWE.