En el artículo anterior, introdujimos la idea visual de los retículos: cuadrículas multidimensionales donde problemas como encontrar el vector más corto (SVP) son convencionalmente intratables.

Ilustración de un retículo criptográfico, una 'cuadrícula multidimensional' base de los problemas post-cuánticos.
Ahora, avanzamos al Capítulo 4: Fundamentos Modernos del paper de Peikert. Este capítulo es el núcleo teórico que explica cómo los criptógrafos transformaron la "dificultad" de los retículos en herramientas funcionales. Lo lograron definiendo dos problemas fundamentales: SIS (Short Integer Solution) y LWE (Learning With Errors).
SIS (Short Integer Solution): La Base de las Firmas
El paper introduce primero el problema SIS, o "Solución Entera Corta", como la base para primitivas criptográficas como las funciones hash resistentes a colisiones y las firmas digitales.
El Problema
Imagina que te doy una matriz A llena de vectores aleatorios (la clave pública). Tu desafío es encontrar un vector z (la solución) que cumpla dos condiciones:
- Resuelve la ecuación: A ⋅ z = 0 (mod q) (es decir, encontrar una combinación de los vectores de A que, al sumarlos, te devuelvan al origen).
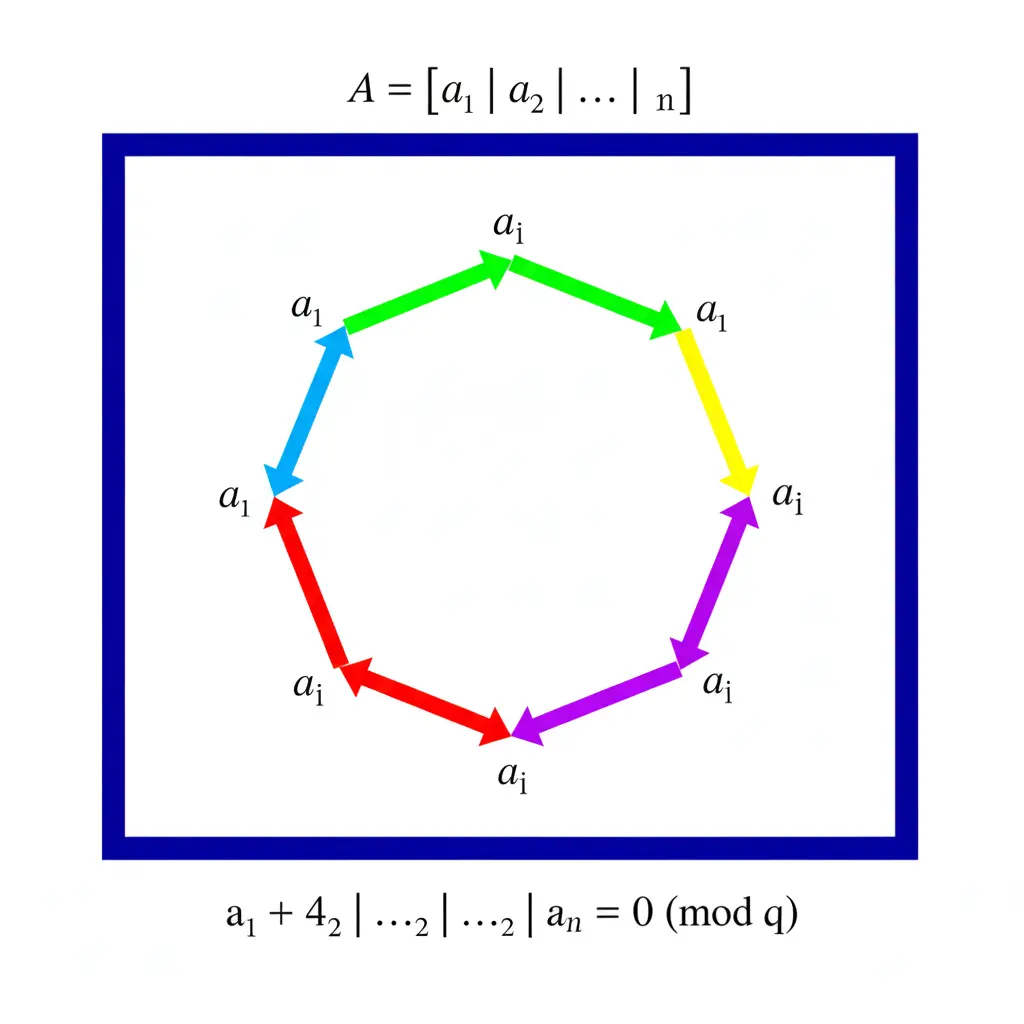
El problema SIS: Encontrar una combinación de vectores A que, al sumarlos, "devuelvan al origen" (A * z = 0 (mod q)).
- Es "Corta": El vector z no puede ser trivial. Sus componentes deben ser enteros pequeños, cumpliendo ‖z‖ ≤ β (donde β es un límite de norma pequeño).
Sin la segunda condición (ser "corta"), el problema es fácil de resolver usando álgebra lineal básica (eliminación de Gauss). Pero añadir la restricción de "corto" lo vuelve intratable.
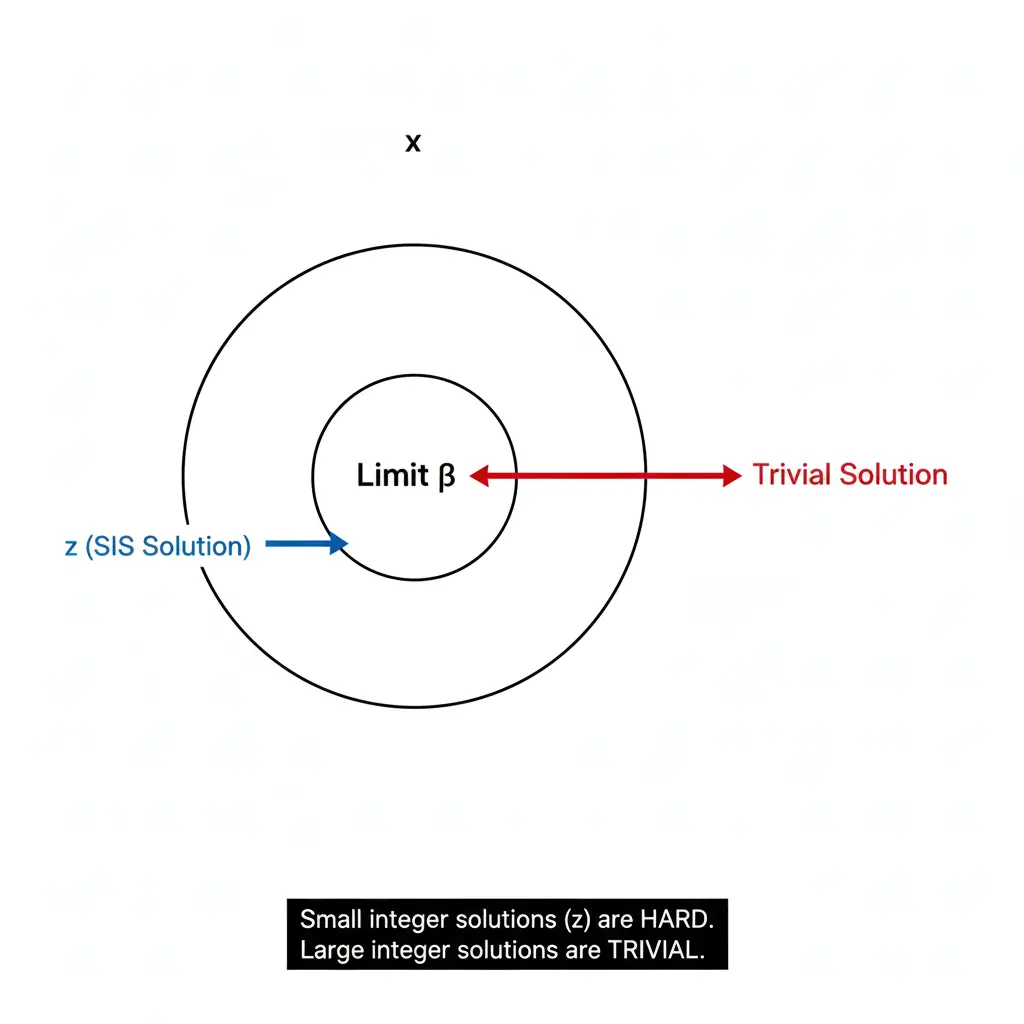
La dificultad de SIS: Las soluciones 'cortas' (vector z) dentro del límite β son intratables, mientras que las soluciones triviales (grandes) son fáciles.
La Conexión Criptográfica: Resistencia a Colisiones
¿Por qué es esto útil? Porque el paper nos muestra que SIS es la base de la resistencia a colisiones.
Se puede definir una función hash f_A(z) = A ⋅ z. Encontrar una "colisión" (dos entradas diferentes z₁ y z₂ tal que f_A(z₁) = f_A(z₂)) es matemáticamente equivalente a encontrar una solución corta z = z₁ − z₂ para el problema SIS.
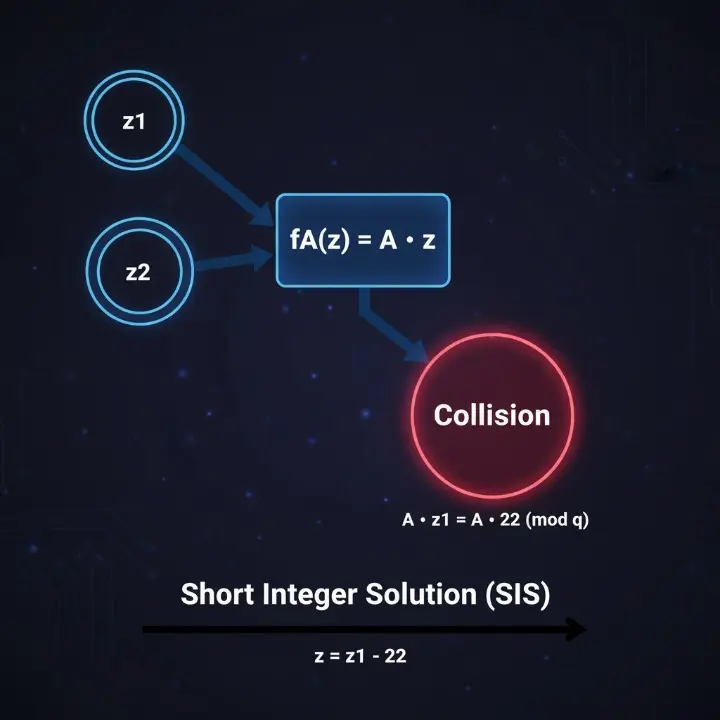
SIS crea resistencia a colisiones. Encontrar una colisión (f_A(z1) = f_A(z2)) es matemáticamente equivalente a encontrar una solución corta z.
Como creemos que SIS es difícil, hemos creado una función hash para la cual es imposible encontrar colisiones. Esta es la propiedad fundamental necesaria para crear firmas digitales seguras.
En Resumen (SIS):
- El Problema: Encontrar una combinación corta de vectores públicos que sume cero.
- El Uso: Proporciona resistencia a colisiones, la base para las firmas digitales post-cuánticas.
- La Seguridad: Es al menos tan difícil como resolver los problemas de retículos del peor caso (como SVP).
LWE (Learning With Errors): La Base del Cifrado
El segundo pilar, introducido por Oded Regev en 2005, es "Learning With Errors" (Aprendizaje con Errores), descrito en la Sección 4.2. El paper lo presenta como el "análogo de SIS que habilita el cifrado".
El Problema
LWE es un juego de distinción. Se te presenta una serie de pares de vectores (a,b) y debes decidir cuál de estos dos "mundos" generó los datos:
- Mundo 1 (Aleatorio): Los pares (a,b) son uniformemente aleatorios. a y b no tienen ninguna relación.
- Mundo 2 (LWE): Los pares siguen una regla secreta. Hay un vector secreto s (la clave privada). El vector b se calcula como b = ⟨s, a⟩ + e (mod q).
La e es un vector de "error" pequeño o "ruido", generalmente muestreado de una distribución Gaussiana.
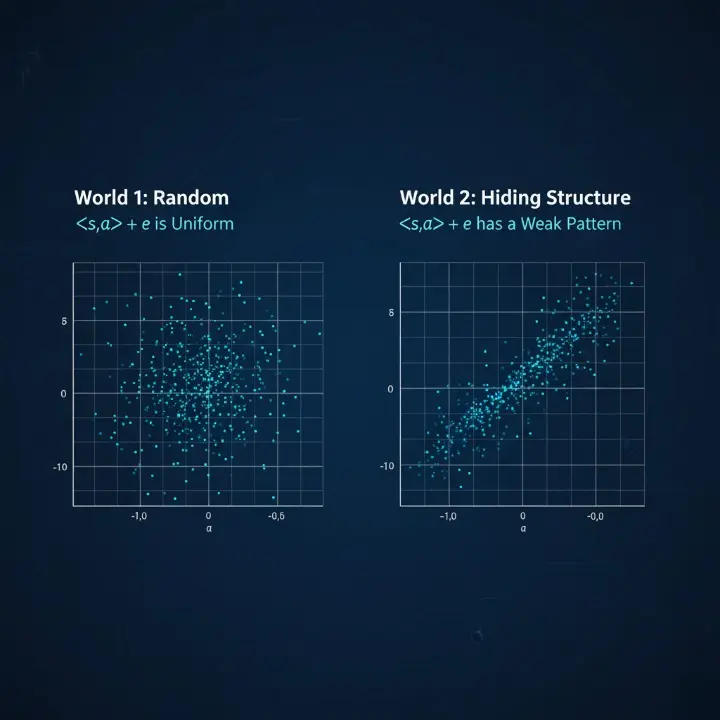
El desafío LWE: Distinguir entre datos puramente aleatorios (Mundo 1) y datos que ocultan un secreto s con 'ruido' (Mundo 2).
La Conexión Criptográfica: Cifrado de Clave Pública
El paper explica en la Sección 4.2.3 que este problema es un criptosistema de clave pública.
- Sin el error e, el problema sería trivial. Un atacante podría usar álgebra lineal para encontrar el secreto s rápidamente.
- Con el error e, el problema se vuelve tan difícil como los problemas de retículos del peor caso.
El "ruido" e actúa como el mecanismo de cifrado. Los pares (a,b) (las muestras de LWE) forman la clave pública: parecen totalmente aleatorios para cualquiera, pero ocultan una relación secreta. El mensaje μ se puede codificar dentro del error e.
Cualquiera puede usar la clave pública (a,b) para cifrar, pero solo la persona que posee el secreto s puede "restar" el término ⟨s, a⟩ y quedarse solo con el error e, que contiene el mensaje original.
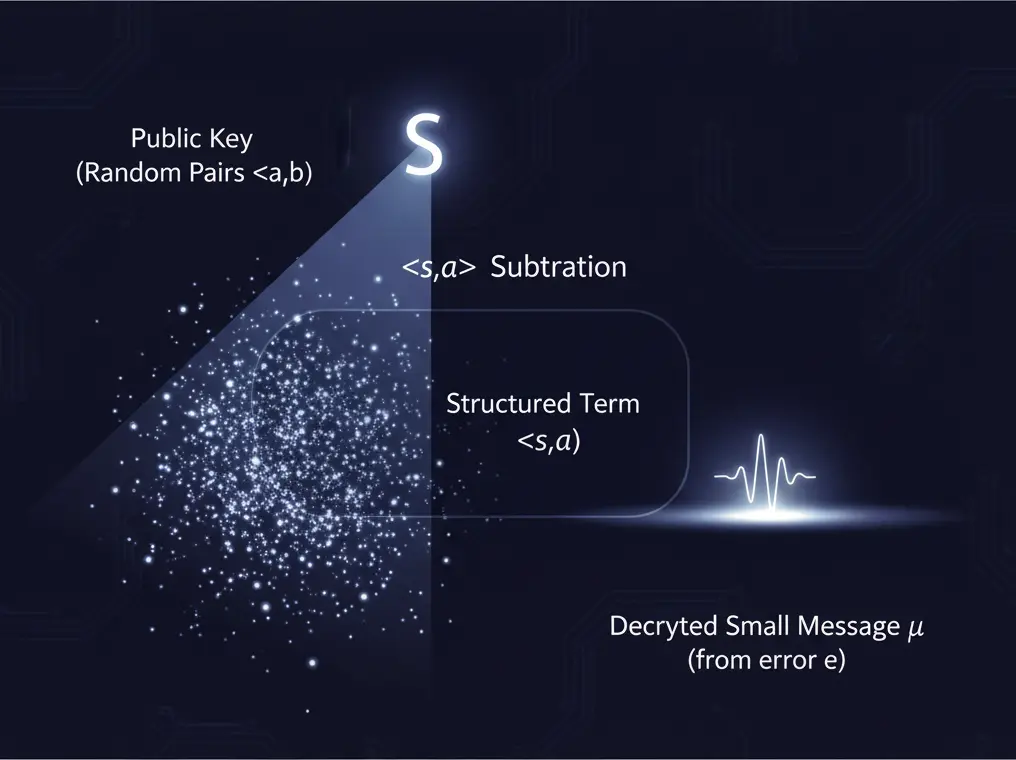
Descifrado LWE: Quien posee el secreto s puede 'restar' el término <s, a> para aislar el error e, que contiene el mensaje original μ .
En Resumen (LWE):
- El Problema: Distinguir entre pares (a,b) aleatorios y pares (a,b) que ocultan un secreto s mediante un pequeño "ruido" e.
- El Uso: Proporciona pseudoraleatoriedad, la base para el cifrado de clave pública post-cuántico.
- La Seguridad: Es al menos tan difícil como resolver los problemas de retículos del peor caso.
Conclusión
Ahora tenemos nuestros dos pilares modernos. SIS nos da una forma de construir funciones hash y firmas (resistentes a colisiones), y LWE nos da una forma de construir cifrado (basado en la indistinguibilidad del ruido).
Sin embargo, estos problemas en su forma pura tienen un inconveniente: la matriz A y el número de muestras m son muy grandes, lo que genera claves públicas enormes e ineficientes.
En el próximo artículo, veremos cómo el paper soluciona esto en las Secciones 4.3 y 4.4 usando "anillos" para crear Ring-LWE y Module-LWE, haciendo que esta teoría sea lo suficientemente rápida y compacta para el mundo real.